By the end of the lesson I will be able to:
Before studying this lesson I need to make sure that I know how to:
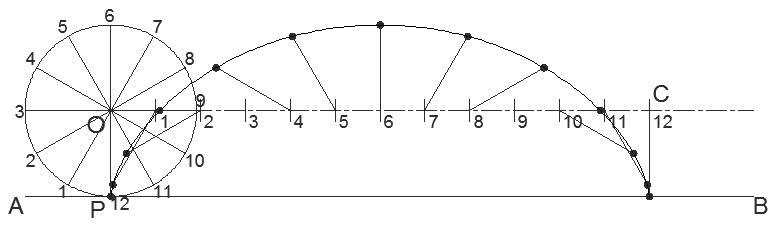
Note that the line forming the cycloid is the green one as it is the one that lies on the circumference.

Step 1: Draw the generating circle, the base line and the centre lines. Mark off point 'P'. Notice the centre line has been extended parallel to the base line. Draw everything faint.

Step 2: Divide the circle into 12 parts at 30° intervals. Add numbers.

Step 3: When the circle makes one whole revolution it will travel a distance equal to its circumference. Mark this distance off on the centre line as shown so that the distance 'OC' is equal to the circumference. Divide 'OC' into 12 equal parts. Add numbers.
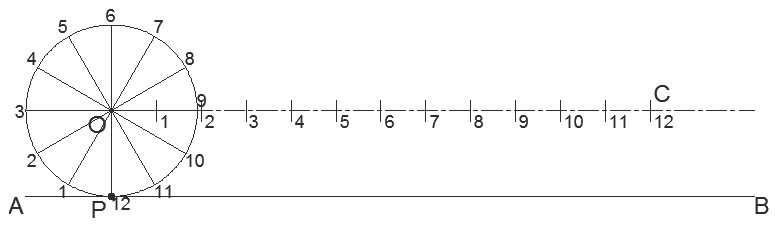
NOTE: If you imagine the circle as it makes 1/12th of a revolution, its centre will move from 'O' to point '1' on the centre line. Also, after 1/12th of a revolution, the radius 'OP' will rotate 30°; so when the circle's centre is at '1', radius 'OP' is oriented parallel to 'O1' as shown.

Step 4: Mark off the radii on the centre line representing every 1/12th step of the revolution. Make sure to draw them parallel to the corresponding number on the circle.

Step 5: The cycloid required goes through the 12 points at the end of each radius. Draw freehand a line going through the 12 points marked off. This is one revolution of your cycloid!